Парапланеризм для «чайников»

Объясняем понятие «Интеграл»

Процесс нахождения производной называется дифференцированием, а нахождение первообразной – интегрированием.

Интеграл записывается так:

Каждая подынтегральная функция умножается на компонент «dx». Он показывает, по какой переменной осуществляется интегрирование. «dx» – это приращение аргумента. Вместо X может быть любой другой аргумент, например t (время).

Неопределённый интеграл

Неопределенный интеграл не имеет границ интегрирования.

Для решения неопределённых интегралов достаточно найти первообразную подынтегральной функции и прибавить к ней «C».

Определённый интеграл

В определенном интеграле на знаке интегрирования пишут ограничения «a» и «b». Они указаны на оси X в графике ниже.

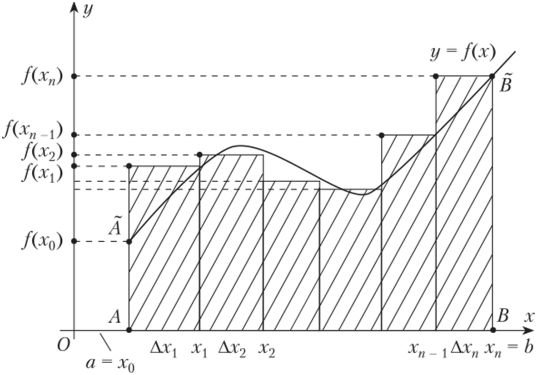
Точки A и B на оси X – есть ограничение зоны определения интеграла

Для вычисления определенного интеграла необходимо найти первообразную, подставить в неё значения «a» и «b» и найти разность. В математике это называется формулой Ньютона-Лейбница:

О книге

В современном мире, регулярно сталкиваясь с потоком негативной информации и отрицательных эмоций, человек должен уметь “восстанавливаться” и отдыхать от повседневных забот. Один из самых действенных и популярных способов – чтение книг. Благодаря волшебной способности книг переносить читателя в другие миры, появляется прекрасная возможность забыться о деловых неурядицах и личных проблемах.

Одной из заметных произведений, написанных в жанре физические науки. астрономия, является работа Маран Стивен П. «Астрономия для “чайников”»

Обращая внимание на многие глубокие вопросы современности, автор делится с нами своими ощущениями и переживаниями. Незаурядная сюжетная линия, интересные персонажи и тонко описанные пейзажи произведения без сомнения увлекут и захватят читателя

На что стоит обратить внимание

Но не менее важно обращать внимание на следующие нюансы:

спокойствие и сосредоточенность – начиная маневр, сосредоточьтесь только на его выполнении, не реагируйте на тех, кто захочет вас поторопить;
не пренебрегайте внутренними и боковыми зеркалами – постоянно поворачиваясь назад или открывая двери, вы не только можете потерять контроль над ситуацией, но еще и повредить, стоящие рядом автомобили;
учитывайте, что машина с задним приводом имеет минимальный радиус поворота, а полноприводный автомобиль – максимальный;
обращайте внимание на запрещающие парковку знаки, даже если в выбранном вами месте для стоянки уже припаркованы другие автомобили – нарушение правил остановки или стоянки автомобиля грозит его владельцу штрафами (КоАП РФ, ст. 12.19) или эвакуацией (КоАП РФ, ст

27.13);
проследите за тем, чтобы выбранное вами место не являлось пешеходной дорожкой или выездом со двора.

Задним ходом

Параллельную парковку задним ходом в условиях города необходимо выполнять поэтапно:

1. Выбор места. Необходимо научиться визуально оценивать место возможной парковки и соотносить его с габаритами своего автомобиля.

   Не знаете как выполнить это на глаз? Считайте бордюрные камни.

2. Начало маневра.
3. Движение задним ходом.
4. Завершение параллельной парковки.

Передним ходом

Зачастую движение задним ходом вызывает у водителей-новичков определенные трудности.

На самом деле существуют определенные секреты и хитрости, которые могут вам вместить свой автомобиль между двумя уже припаркованными, двигаясь вперед:

1. Найдя подходящее место для парковки, заезжайте в него передом, влезая передним правым колесом на обочину.
2. Двигайтесь вперед до тех пор, пока заднее правое колесо машины не поравняется с тротуаром (обочиной). После этого выверните руль влево и двигайтесь назад, чтобы спустить авто с тротуара.

Помните, что подобный метод парковки довольно опасен:

• вы можете повредить автомобиль о слишком высокий бордюрный камень;
• получить штраф в 1000 рублей за заезд на тротуар (КоАП РФ, ст. 12.19);
• повредить свой автомобиль или чужое имущество.

Хотите узнать, что собой представляет парковка для резидента? Смотрите об этом в статье: резидентская парковка. О том, каков нормативный размер парковка, написано здесь.

Действия с векторами. Коллинеарность векторов

В школьном курсе геометрии рассматривается ряд действий и правил с векторами: сложение по правилу треугольника, сложение по правилу параллелограмма, правило разности векторов, умножения вектора на число, скалярное произведение векторов и др. Для затравки повторим два правила, которые особенно актуальны для решения задач аналитической геометрии.

Правило сложения векторов по правилу треугольников

Рассмотрим два произвольных ненулевых вектора  и :

Требуется найти сумму данных векторов. В силу того, что все векторы считаются свободными, отложим вектор  от конца вектора :

Суммой векторов  и  является вектор . Для лучшего понимания правила в него целесообразно вложить физический смысл: пусть некоторое тело совершило путь по вектору , а затем по вектору . Тогда сумма векторов  представляет собой вектор результирующего перемещения  с началом в точке отправления и концом в точке прибытия. Аналогичное правило формулируется для суммы любого количества векторов. Как говорится, тело может пройти свой путь сильно поддатым по зигзагу, а может и на автопилоте – по результирующему вектору суммы.

Кстати, если вектор  отложить от начала вектора , то получится эквивалентное правило параллелограмма сложения векторов.

Умножение вектора на число

Сначала о коллинеарности векторов. Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Грубо говоря, речь идёт о параллельных векторах. Но применительно к ним всегда используют прилагательное «коллинеарные».

Представьте два коллинеарных вектора. Если стрелки данных векторов направлены в одинаковом направлении, то такие векторы называются сонаправленными. Если стрелки смотрят в разные стороны, то векторы будут противоположно направлены.

Обозначения: коллинеарность векторов записывают привычным значком параллельности: , при этом возможна детализация:  (векторы сонаправлены) или  (векторы направлены противоположно).

Произведением ненулевого вектора  на число  является такой вектор , длина которого равна , причём векторы   и  сонаправлены при  и противоположно направлены при .

Правило умножения вектора на число легче понять с помощью рисунка: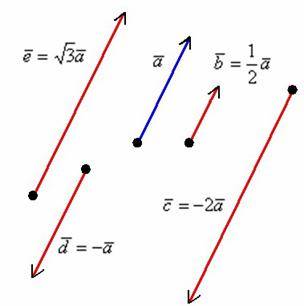

Разбираемся более детально:

1) Направление. Если множитель  отрицательный,  то вектор меняет направление на противоположное.

2) Длина. Если множитель заключен в пределах  или , то длина вектора уменьшается. Так, длина вектора  в два раза меньше длины вектора . Если множитель  по модулю больше единицы, то длина вектора увеличивается в  раз.

3) Обратите внимание, что все векторы коллинеарны, при этом один вектор выражен через другой, например,. Обратное тоже справедливо: если один вектор можно выразить через другой, то такие векторы обязательно  коллинеарны

Таким образом: если мы умножаем вектор на число, то получится коллинеарный (по отношению к исходному) вектор.

4) Векторы  сонаправлены. Векторы  и  также сонаправлены. Любой вектор первой группы противоположно направлен по отношению к любому вектору второй группы.

Какие векторы являются равными?

Два вектора равны, если они сонаправлены и имеют одинаковую длину. Заметьте, что сонаправленность подразумевает коллинеарность векторов. Определение будет неточным (избыточным), если сказать: «Два вектора равны, если они коллинеарны, сонаправлены и имеют одинаковую длину».

С точки зрения понятия свободного вектора, равные векторы – это один и тот же вектор, о чём уже шла речь в предыдущем параграфе.

Интеграл – что это?

Предпосылки. Потребность в интегрировании возникла в Древней Греции. В то время Архимед начал применять для нахождения площади окружности методы, похожие по сути на современные интегральные исчисления. Основным подходом для определения площади неровных фигур тогда был «Метод исчерпывания», который достаточно лёгок для понимания.

Суть метода. В данную фигуру вписывается монотонная последовательность других фигур, а затем вычисляется предел последовательности их площадей. Этот предел и принимался за площадь данной фигуры.

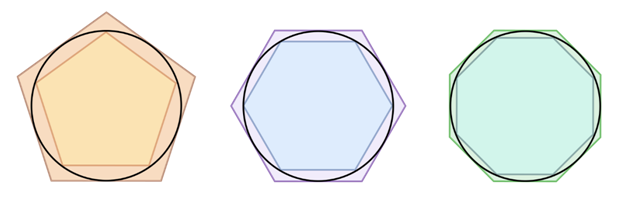
Метод исчерпывания для определения площади круга

В этом методе легко прослеживается идея интегрального исчисления, которая заключается в нахождении предела бесконечной суммы. В дальнейшем эта идея применялась учёными для решения прикладных задач астронавтики, экономики, механики и др.

Современный интеграл. Классическая теория интегрирования была сформулирована в общем виде Ньютоном и Лейбницем. Она опиралась на существовавшие тогда законы дифференциального исчисления. Для её понимания, необходимо иметь некоторые базовые знания, которые помогут математическим языком описать визуальные и интуитивные представления об интегралах.

Понятие предела в математике

Первый вопрос: что это вообще за предел и предел чего? Можно говорить о пределах числовых последовательностей и функций. Нас интересует понятие предела функции , так как именно с ними чаще всего сталкиваются студенты. Но сначала – самое общее определение предела:

Звучит громоздко, но записывается очень просто:

Lim – от английского limit – предел.

Существует также геометрическое объяснение определения предела, но здесь мы не будем лезть в теорию, так как нас больше интересует практическая, нежели теоретическая сторона вопроса. Когда мы говорим, что х стремится к какому-то значению, это значит, что переменная не принимает значение числа, но бесконечно близко к нему приближается.

Приведем конкретный пример. Задача – найти предел.

Чтобы решить такой пример, подставим значение x=3 в функцию. Получим:

Кстати, если Вас интересуют базовые операции над матрицами, читайте отдельную статью на эту тему.

В примерах х может стремиться к любому значению. Это может быть любое число или бесконечность. Вот пример, когда х стремится к бесконечности:

Интуитивно понятно, что чем больше число в знаменателе, тем меньшее значение будет принимать функция. Так, при неограниченном росте х значение 1/х будет уменьшаться и приближаться к нулю.

Как видим, чтобы решить предел, нужно просто подставить в функцию значение, к которому стремиться х. Однако это самый простой случай. Часто нахождение предела не так очевидно. В пределах встречаются неопределенности типа 0/0 или бесконечность/бесконечность. Что делать в таких случаях? Прибегать к хитростям!

Почему вы не знаете, как решать интегралы

А для чего нужны интегралы? Попробуйте сами себе ответить на этот вопрос.

Объясняя тему интегралов, учителя перечисляют малополезные школьным умам области применения. Среди них:

• вычисление площади фигуры.
• вычисление массы тела с неравномерной плотностью.
• определение пройденного пути при движении с непостоянной скоростью.
• и др.

Связать все эти процессы не всегда получается, поэтому многие ученики путаются, даже при наличии всех базовых знаний для понимания интеграла.

Главная причина незнания – отсутствие понимания практической значимости интегралов.

Нужна помощь в написании работы?

Мы – биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.

Правила

Чтобы уверенно и правильно выполнять параллельную парковку в любом месте, необходимо хорошо запомнить правила и алгоритм маневра.

В городе

Если вы решили попрактиковаться и припарковаться в городе, необходимо пошагово выполнять следующую инструкцию:

1. Проехать выбранное место для парковки и остановиться параллельно припаркованному автомобилю.
2. Повернуть руль вправо, включить заднюю передачу и начать передвижение.
3. Контролируйте собственное передвижение по зеркалам. Остановите движение, когда в водительское зеркало увидите передние фары сзади стоящего автомобиля.
4. Поставьте рулевое колесо прямо и продолжайте движение назад, пока не увидите бампер впереди стоящей машины.
5. Выровняйте свое авто между двумя автомобилями.

Параллельная парковка на автодроме

Алгоритм параллельной парковки на тренировочной площадке выглядит следующим образом:

1. Подъехать к разметке «Старт» и остановиться.
2. По сигналу начать движение вперед и остановиться у крайней фишки, обозначающий впереди стоящий припаркованный автомобиль.
3. Вывернуть руль вправо и начать движение назад, следя за правым боковым зеркалом.
4. Остановить движение в момент, когда в левое зеркало вы увидите фишку, обозначающую правый передний угол автомобиля, припаркованного сзади.
5. Повернуть руль прямо и начать движение назад, загоняя машину на парковочное место.

Сложности

Маневр параллельная парковка является одним из самых сложных для исполнения и в то же время очень востребованным в условиях вождения в городах.

Но даже пройдя курс обучения и обладая определенными навыками вождения не стоит забывать о главных трудностях, возникающих при проведении этого маневра в реальной жизни:

непонимание габаритов своего авто – важно учитывать не только размеры парковочного места, но и расстояния между всеми автомобилями, чтобы избежать ДТП и повреждений автомобилей;
неумение пользоваться зеркалами заднего вида – прежде чем приступать к выполнению такого сложного маневра, необходимо «приноровиться» к своим зеркалам, ведь в некоторых случаях они немного искажают реальность, увеличивая или уменьшая картинку;
попытки загнать машину на стоянку в два приема – лихо, крутя руль, не останавливаясь и не вспоминая правильный алгоритм выполнения маневра, можно легко попасть в неприятности и стать главным участником ДТП.

Не знаете, как правильно наносится разметка на стоянку? Смотрите об этом в статье: разметка парковки. О том, как узнать номер парковки, написано тут.

Детально про знаки парковка, расписано здесь.

Параллельная парковка: пошаговая инструкция

Парковочное место в городе обычно располагается между двумя машинами. Хорошо, если пространства хватает для обычного маневра. Но если место ограничено, остается только следовать пошаговой инструкции параллельной парковки для начинающих:

1. Включите правый поворотник и убедитесь, что в заднем зеркале отсутствуют пешеходы и велосипедисты.
2. По ровной линии встаньте рядом с машиной, за которой собираетесь припарковаться.
3. Медленно и плавно начинайте сдавать назад, держа руль максимально повернутым вправо.
4. Смотрите в правое зеркало: когда увидите в нем правую фару машины, которая стоит сзади, остановитесь и верните руль в исходное положение.
5. Выверните руль максимально влево и продолжайте сдавать назад, пока не встанете параллельно.

Скорее всего, вам не удастся закончить маневр в легендарные «три действия». Не отчаивайтесь и попробуйте встать максимально близко к поребрику, двигаясь в ограниченном пространстве парковочного места. Со временем вы научитесь осуществлять этот сложный маневр быстро и легко.

С этой книгой читают

Астрономия для всехКоротцев О. Н, Коротцев О. В.

Эта замечательная книга повествует о новейших открытиях и достижениях в изучении Вселенной. Стремительному развитию астрономии в наши дни способствуют космические…

4.5
 (2)

Развитие памяти для чайниковДжон Богосиан Арден

Итак, вы хотите улучшить свою память. Универсального метода улучшения памяти не существует. С увеличением количества изученных и отработанных способов, используемых для…

4.67
 (3)

Заметки чайника-мага Шмат Арсен Станиславович

Называется, зашел в магазин купить газировки, а в результате оказался в другом мире.

И так, что мы имеем? Огромный уровень магических способностей, знания родного…

3.7
 (2)

Астрономия и космос. ЭнциклопедияМайлс Лайза, Смит Алистер

Эта богато иллюстрированная книга покажет Вам Вселенную на основе последних увлекательных сообщений от астрономов всей планеты и космичесикх зондов.

Для среднего…

Гитара для “чайников”Чаппел Джон, Филипс Марк

Данная книга представляет собой вводный курс по самостоятельному изучению приёмов игры на гитаре. В ней приведены базовые сведения, необходимые для исполнения…

5
 (4)

Магия для чайников Jane Porter

Где я? Что это за место? Везде темно, пусто. Только мелькают какие-то всполохи. Я умер? Кто я такой? Что я такое? Кем я был? Зачем мне это знать? Я хочу это знать?…

3.5
 (4)

Физика для “чайников” Задумавшийся Андрей

От автора В школьные годы меня очень раздражало то, что учебники по всем предметам пишутся сухим академическим языком, и читать такие учебники, не имея представления о…

4.3
 (5)

C++ для “чайников”Стефан Рэнди Дэвис

C++ для “чайников” 4-е издание.

***   ***   ***

“Моим друзьям и семье, которые помогли мне

стать “чайником ” в еще большей степени,

чем я есть на самом…

3.52
 (5)

Понятие вектора. Свободный вектор

Сначала повторим школьное определение вектора. Вектором называется направленный отрезок, для которого указано его начало и конец:
В данном случае началом отрезка является точка , концом отрезка – точка . Сам вектор обозначен через . Направление имеет существенное значение, если переставить стрелку в другой конец отрезка, то получится вектор , и это уже совершенно другой вектор. Понятие вектора удобно отождествлять с движением физического тела: согласитесь, зайти в двери института или выйти из дверей института – это совершенно разные вещи.

Отдельные точки плоскости, пространства удобно считать так называемым нулевым вектором . У такого вектора конец и начало совпадают.

!!! Примечание: Здесь и далее можете считать, что векторы лежат в одной плоскости или можете считать, что они расположены в пространстве – суть излагаемого материала справедлива и для плоскости и для пространства.

Обозначения: Многие сразу обратили внимание на палочку без стрелочки в обозначении  и сказали, там же вверху еще стрелку ставят! Верно, можно записать со стрелкой: , но допустима и запись , которую я буду использовать в дальнейшем. Почему? Видимо, такая привычка сложилась из практических соображений, слишком разнокалиберными и мохнатыми получались мои стрелки в школе и ВУЗе

В учебной литературе иногда вообще не заморачиваются клинописью, а выделяют буквы жирным шрифтом: , подразумевая тем самым, что это вектор.

То была стилистика, а сейчас о способах записи векторов:

1) Векторы можно записать двумя большими латинскими буквами: и так далее. При этом первая буква обязательно обозначает точку-начало вектора, а вторая буква – точку-конец вектора.

2) Векторы также записывают маленькими латинскими буквами: В частности, наш вектор  можно для краткости переобозначить маленькой латинской буквой .

Длиной или модулем ненулевого вектора  называется длина отрезка . Длина нулевого вектора  равна нулю. Логично.

Длина вектора обозначается знаком модуля: ,

Как находить длину вектора мы узнаем (или повторим, для кого как) чуть позже.

То были элементарные сведения о векторе, знакомые всем школьникам. В аналитической же геометрии рассматривается так называемый свободный вектор.

Если совсем просто – вектор можно отложить от любой точки: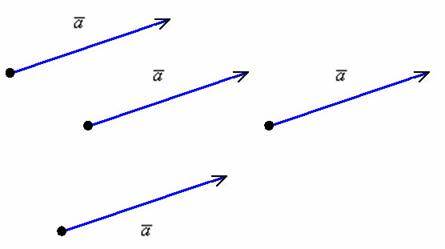

Такие векторы мы привыкли называть равными (определение равных векторов будет дано ниже), но чисто с математической точки зрения это ОДИН И ТОТ ЖЕ ВЕКТОР или свободный вектор. Почему свободный? Потому что в ходе решения задач вы можете «пристроить» тот или иной «школьный» вектор в ЛЮБУЮ, нужную вам точку плоскости или пространства. Это очень крутое свойство! Представьте направленный отрезок произвольной длины и направления – его можно «клонировать» бесконечное количество раз и в любой точке пространства, по сути, он существует ВЕЗДЕ. Есть такая студенческая присказка: Каждому лектору в ж**у по вектору. Ведь не просто остроумная рифма, всё почти корректно – направленный отрезок можно пристроить и туда. Но не спешите радоваться, чаще страдают сами студенты =)

Итак, свободный вектор – это множество одинаковых направленных отрезков. Школьное определение вектора, данное в начале параграфа: «Вектором называется направленный отрезок…», подразумевает конкретный направленный отрезок, взятый из данного множества, который привязан к определённой точке плоскости или пространства.

Следует отметить, что с точки зрения физики понятие свободного вектора в общем случае некорректно, и точка приложения имеет значение. Действительно, прямой удар одинаковой силы по носу или по лбу хватит развивать мой дурацкий пример влёчет разные последствия. Впрочем, несвободные векторы встречаются и в курсе вышмата (не ходите туда :)).

Далее, если не оговаривается иное, речь пойдёт только о свободных векторах.

Распространённые ошибки

Приведены самые частые ошибки водителей:

1. Ученики слишком близко прижимаются к левому краю разметки, чтобы минимизировать в будущем процесс выравнивания и максимально правильно встать с первого выкручивания, Это чревато тем, что при сдавании назад можно случайно сбить флажок или выехать за пределы линии. На экзамене это, конечно, кажется мелочью, но в жизни такая неаккуратность привела бы к порче своего и чужого авто, поэтому за неё очень сильно штрафуют.
2. Не полный поворот руля. Для того, чтобы максимально правильно встать с первого раза, необходимо при повороте полностью выворачивать руль. Это позволит облегчить процесс выравнивания, однако многие этим пренебрегают. Конечно, конкретно за это в автошколах не штрафуют, но такая невнимательность может обернуться потерей времени, которое, как известно, на экзамене ограничено.
3. Не полное пересечение боковой линии. Как было сказано ранее, автомобиль не должен выпирать из общего ряда машин, а если обозначена линия пересечена не полностью, именно это и случиться на дороге, а значит основное движение будет затруднено.

Базовые понятия для понимания темы

Чтобы вы поняли суть интегрирования и не закрыли страницу от непонимания, мы объясним ряд базовых понятий. Что такое функция, производная, предел и первообразная.

Функция – правило, по которому все элементы из одного множества соотносятся со всеми элементами из другого.

Производная – функция, описывающая скорость изменения другой функции в каждой конкретной точке. Если говорить строгим языком, – это предел отношения приращения функции к приращению аргумента. Он вычисляется вручную, но проще использовать таблицу производных, в которой собрано большинство стандартных функций.

Приращение – количественное изменение функции при некотором изменении аргумента.

Предел – величина, к которой стремиться значение функции, при стремлении аргумента к определённому значению.

Пример предела: допустим при X равном 1, Y будет равно 2. Но что, если X не равен 1, а стремится к 1, то есть никогда её не достигает? В этом случае y никогда не достигнет 2, а будет только стремиться к этой величине. На математическом языке это записывается так: limY(X), при X –> 1 = 2. Читается: предел функции Y(X), при x стремящемся к 1, равен 2.

Как уже было сказано, производная – это функция, описывающая другую функцию. Изначальная функция может быть производной для какой-либо другой функции. Эта другая функция называется первообразной.